Estimation of Value of Pi in Diffrent Dimension

Estimation of Value of Pi From Area of Circle in Two Dimension Using Monte Carlo

Here, we have value of hypersphere in n dimension

\[V_n(R) = \frac{\pi^\frac{n}{2}}{\frac{n}{2}!}R^n\]

When n = 2, then above equation becomes, \(V_2(R) = \frac{\pi^\frac{2}{2}}{\frac{2}{2}!}R^2\) \(V_2(R) = \pi R^2\)

In a 2-D plane, the goal is to mimic random (x, y) points with a domain that is a square of 2r units centered on (0,0). Consider an inscribed square-shaped circle with the same radius r inside the same domain. The ratio between the number of points inside the circle and the overall number of generated points is then determined.

In our case r = 1 radius of circle

L = 2r length of square

v = L^2 volume of square = 4

In 2D

v = 𝜋𝑅2

𝜋 = 4

import random
import math
import numpy as np
import matplotlib.pyplot as plt

N = [100,1000,10000,100000,100000]
E = []

true_value = 3.141592
for j in range(len(N)):
    c= 0
    s = 0
    I = 0
    
    for i in range(N[j]):
        x = random.random()
        y = random.random()
        d = x*x + y*y
        if d <= 1:
            c +=1
        s +=1
        I += 1

    pi = 4 * (c/s)
    print(f'Calculated value of pi: {pi}')
    error = abs(pi - true_value)
    print(f'Estimated value of error: {error}')
    E.append(error)
    

    

    
    
    
    
    

Calculated value of pi: 3.04
Estimated value of error: 0.10159200000000013
Calculated value of pi: 3.164
Estimated value of error: 0.022407999999999983
Calculated value of pi: 3.1504
Estimated value of error: 0.008807999999999705
Calculated value of pi: 3.14332
Estimated value of error: 0.0017279999999999518
Calculated value of pi: 3.1496
Estimated value of error: 0.008007999999999793

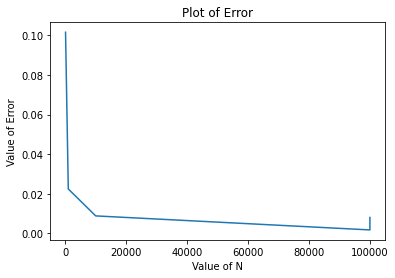
Plot of Number VS Error

plt.plot(N,E)
plt.title("Plot of Error")
plt.xlabel("Value of N")
plt.ylabel("Value of Error")

Text(0, 0.5, 'Value of Error')

Estimation of Value of Pi From Volume of Sphere in Three Dimension

Here, we have value of hypersphere in n dimension

\[V_n(R) = \frac{\pi^\frac{n}{2}}{\frac{n}{2}!}R^n\]

When n = 3, then above equation becomes, \(V_3(R) = \frac{\pi^\frac{3}{2}}{\frac{3}{2}!}R^3\) \(V_3(R) =0.752252 \pi^\frac{3}{2} R^3\)

In our case r = 1 radius of circle

L = 2r length of square

v = L^3 volume of square = 8

In 3D

v = 4/3𝜋𝑅3

8 = 4/3 𝜋

𝜋 = 6

import random
N = [100,1000,10000,100000]
E = []
true_value = 3.14
for i in range(len(N)):
        I = 0
        for j in range(N[i]):
            x = random.random()
            y = random.random()
            z = random.random()

            r = x**2 + y**2+ z**2
            if r<1:
                I = I + 1



        ratio = I/N[i]
        Pi = ratio * 6
        print(f'Calculated value of pi: {Pi}')
        error = abs(Pi - true_value)
        print(f'Estimated value of error: {error}')
        E.append(error)
                

Calculated value of pi: 3.24
Estimated value of error: 0.10000000000000009
Calculated value of pi: 3.186
Estimated value of error: 0.04599999999999982
Calculated value of pi: 3.189
Estimated value of error: 0.04899999999999993
Calculated value of pi: 3.1386000000000003
Estimated value of error: 0.0013999999999998458

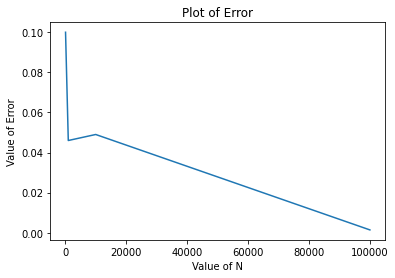
Plot of Number VS Error

plt.plot(N,E)
plt.title("Plot of Error")
plt.xlabel("Value of N")
plt.ylabel("Value of Error")

Text(0, 0.5, 'Value of Error')

Estimation of Value of Pi From Area of Circle in Four Dimension

Here, we have value of hypersphere in n dimension

\[V_n(R) = \frac{\pi^\frac{n}{2}}{\frac{n}{2}!}R^n\]

When n = 4, then above equation becomes, \(V_4(R) = \frac{\pi^\frac{4}{2}}{\frac{4}{2}!}R^4\) \(V_4(R) = \frac{1}{2}(\pi R^2 )^2\)

In our case r = 1 radius of circle

L = 2r length of square

v = L^3 volume of square = 16

In 4D

v = 1/2 𝜋2𝑅4

16 = 1/2 𝜋2

𝜋 = 32^0.5

Estimation of Value of Pi from the integration function

\(\pi = \int_{0}^1 \frac{1}{1+ x^2}dx\) By Hand

\[= [tan^-(x)]_{0}^1\] \[= tan^-(1) - tan^-(0)\]

\(= \pi - 0\) \(= 3.141592653589793238\)

Estimation of value of pi using Integration Method

Algorithm:

1. Import random

2. Import math

3. Import numpy

4. a = 0

5. b = 1

6. integral = 0

7. i = 0

8. while i < 1000

9. x = random.random()

10. integral += 1/1 + x**2

11. i = i + 1

12. ans = integral* (b-a)/float(N)

13. Print(ans)

N = [100,1000,10000,100000,1000000]
print("True Value of Pi")
true_value = 3.141592653589793238
print(true_value)
Error = []
for i in range(len(N)):
    a = 0
    b = 1
    integral = 0
    for j in range(N[i]):
        x = random.random()
        integral += 4 * 1/(1 + x**2)
        ans = integral * (b-a)/float(N[i])
    error = abs(ans - true_value)
    Error.append(error)
    #print(ans)
    print(f'Calclated Value of Pi : {ans}')
print(f'Error Value of pi: {Error}')

True Value of Pi
3.141592653589793
Calclated Value of Pi : 3.2079305434667744
Calclated Value of Pi : 3.1171874694431705
Calclated Value of Pi : 3.141631082310233
Calclated Value of Pi : 3.138488698353392
Calclated Value of Pi : 3.14167462845529
Error Value of pi: [0.0663378898769813, 0.024405184146622627, 3.8428720440020214e-05, 0.003103955236400946, 8.197486549699207e-05]

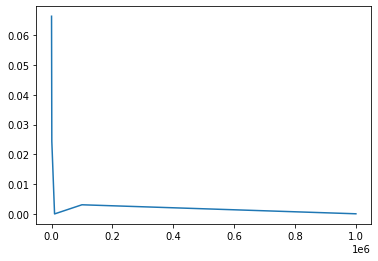
Plot of Number Vs Error

plt.plot(N,E)
plt.title("Plot of Error")
plt.xlabel("Value of N")
plt.ylabel("Value of Error")

[<matplotlib.lines.Line2D at 0x2054093c490>]