K Medoids Clustering in Python from Scratch

Introduction

K-medoids are a prominent clustering algorithm as an improvement of the predecessor, K-Means algorithm. Despite its widely used and less sensitive to noises and outliers, the performance of K-medoids clustering algorithm is affected by the distance function. From here.

When k-means algorithm is not appropriate to make a objects of cluster to the data points then k-medoid clustering algorithm is prefer. The medoid is objects of cluster whose dissimilarity to all the objects in the cluster is minimum. The main difference between K-means and K-medoid algorithm that we work with arbitrary matrix of distance instead of euclidean distance. K-medoid is a classical partitioning technique of clustering that cluster the dataset into k cluster. It is more robust to noise and outliers because it may minimize sum of pair-wise dissimilarities however k-means minimize sum of squared Euclidean distances. Most common distances used in KMedoids clustering techniques are Manhattan distance or Minkowski distance and here we will use Manhattan distance.

We have also written a blog about k-means clustering from scratch. Please read it below:

K means Clustering in Python from Scratch

Manhattan Distance

Of p1, p2 is: $

(x2-x1)+(y2-y1)

Algorithm

Step 1: Randomly select(without replacement) k of the n data points as the median.
Step 2: Associate each data points to the closest median.
Step 3: While the cost of the configuration decreases:
- For each medoid m, for each non-medoid data point o:
  - Swap m and o, re-compute the cost.
  - If the total cost of the configuration increased in the previous step, undo the swap.

## Example Cluster the following data set of ten objects into two clusters i.e. k =3. Data points are ${(1,3),(4,5),(6,3),(3,4),(2,1)}$

Solution Let $p_1=(1,3)$ $p_2 =(4,5)$ $p_3 =(6,3)$ $p_4=(3,4)$ $p_5 =(2,1)$ we are going to cluster the data into two cluster using k-medoids algorithm.

Initial Step Let $m_1= p_1=(1,3)$ and $m_2 = p_4 = (3,4)$ are two initial medoid

$ d(m_1, p_2) = mode(x_2-x_1) + mode(y_2-y_1)$

Iteration 1

Calculate distance between clusters centers and each data point.

$d(m_1,p_1) = 0$

$d(m_2,p_1) = 3$

$d(m_1,p_2) = 3 + 2 = 5$

$d(m_2,p_2) = 1 + 1= 2$

$d(m_1,p_3) = 5 + 0 = 5$

$d(m_2,p_3) = 3 + 1 = 4$

$d(m_1,p_5) = 1 + 2= 3$

$d(m_2,p_5) = 1 + 3= 4$

Hence , after cluster formed are

Cluster 1 = {$p_1, p_5$}
Cluster 2 = {$P_2,p_3,p_4$}

Now, Total Cost = ${d(m_1,p_1) +d(m_1,p_5) + d(m_2, p_2) + d(m_2,p_3)+d(m_2,p_4)}$ = {0 + 2 + 4+3} = 9

Iteration 2

Now $m_1 = p_2=(4,5) $ and $m_2 = p_4 =(3,4) $ are two medoid

Let $p_1 =(1,3)$, $p_2 =(4,5)$, $p_3=(6,3)$ and $p_5=(2,1)$.

Calculate distance between new clusters and each data points.

$d(m_1, p_1) = 3 + 2= 5$

$d(m_2, p_1) = 2 + 1= 3$

$d(m_1, p_3) = 2 + 2 = 4$

$d(m_2, p_3) = 3 + 1 = 4$

$d(m_1, p_5) = 2 + 4 = 6 $

$d(m_2, p_5) = 1 + 3= 5$

Thus after second iteration

Cluster 1 = {$p_2, p_3$}
Cluster 2 = {$p_1, p_4, p_5$}

Total cost = ${d(m_1,p_2)+d(m_1,p_3) + d(m_2, p_1) + d(m_2,p_4)+d(m_2,p_5)}$ = 0 + 4 + 3 + 0 + 5 = 12

Total cost = 12.

Here total cost in iteration 2 is greater then in iteration 1 so, we don’t go further.

Coding Part

import numpy as np
import matplotlib.pyplot as plt

plt.style.use("seaborn-whitegrid")

Basic Example

Lets take an example of data points where we have 5 points and we will try to make 2 clusters for those data.

Initially, we will plot our data points by passing x and y coordinates of all points.
Take point 1st and 4rth as initial mediods points or mediods of two clusters.

data = [(1,3),(4,5),(6,3),(3,4),(2,1)]

points = np.array(data)

# print(points)

plt.figure(figsize=(5,5))
plt.scatter(x=points[:,0],y = points[:,1])
plt.title("Initially")
plt.show()

k = 2
c1 = points[0]
c2 = points[1]

plt.figure(figsize=(5,5))
plt.scatter(x=points[:,0],y = points[:,1])
plt.scatter([c1[0],c2[0]],[c1[1],c2[1]],marker="*")
plt.title("Step 1")
plt.show()

png

Make a function manhattan and get_costs to calculate manhattan distance between point and a mediod of cluster and minimum cost between particular data paints and medoids .
Get initial clusters and cost.
Prepare colours for each clusters and show initial clusters.
Now, we will loop until some internal break happens:
- Initially assume that there is no swap happened because if it is the case we must exit from the loop.
- Loop through numbers of sample
  - If current sample is not in medoid, then we will compare this sample’s distance with each of medoids.
  - If We will swap the sample and medoids and calculate its cost. If the cost is smaller than previous cost then we accept the swap and make it true as well as change the clusters. We will also plot the clusters.
  - Else we ignore the swap and move on from there.
- If no swap has happened or we reached the number of iterations, then we exit from the loop.

def manhattan(p1, p2):
    return np.abs((p1[0]-p2[0])) + np.abs((p1[1]-p2[1]))

def get_costs(data, medoids):
    clusters = {i:[] for i in range(len(medoids))}
    cst = 0
    for d in data:
        dst = np.array([manhattan(d, md) for md in medoids])
        c = dst.argmin()
        clusters[c].append(d)
        cst+=dst.min()
        
    clusters = {k:np.array(v) for k,v in clusters.items()}
    return clusters, cst
        

def KMedoids(data, k, iters = 100):
    medoids = np.array([data[i] for i in range(k)])
    samples,_ = data.shape
    
    clusters, cost = get_costs(data, medoids)
    count = 0
    
    colors =  np.array(np.random.randint(0, 255, size =(k, 4)))/255
    colors[:,3]=1
    
    plt.title(f"Step : 0")
    [plt.scatter(clusters[t][:, 0], clusters[t][:, 1], marker="*", s=100,
                                    color = colors[t]) for t in range(k)]
    plt.scatter(medoids[:, 0], medoids[:, 1], s=200, color=colors)
    plt.show()
    
    while True:
        swap = False
        for i in range(samples):
            if not i in medoids:
                for j in range(k):
                    tmp_meds = medoids.copy()
                    tmp_meds[j] = i
                    clusters_, cost_ = get_costs(data, tmp_meds)
                    
                    if cost_<cost:
                        medoids = tmp_meds
                        cost = cost_
                        swap = True
                        clusters = clusters_
                        print(f"Medoids Changed to: {medoids}.")
                        plt.title(f"Step : {count+1}")  
                        [plt.scatter(clusters[t][:, 0], clusters[t][:, 1], marker="*", s=100,
                                    color = colors[t]) for t in range(k)]
                        plt.scatter(medoids[:, 0], medoids[:, 1], s=200, color=colors)
                        plt.show()
        count+=1
        
        if count>=iters:
            print("End of the iterations.")
            break
        if not swap:
            print("No changes.")
            break
                    
            
            
KMedoids(points,2)    

png

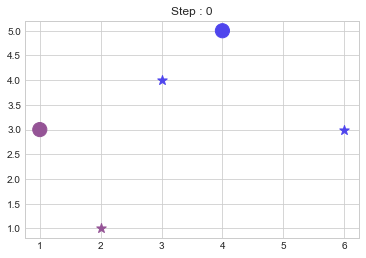
No changes.

Now looking over the output of our code, it seems that it worked pretty well but what if our cluster size is variable and data also varies? So to make our code little bit more awesome, we will do few more tasks.

`KMedoids` Class

Some of reasons that we are using a class are:

To make our code dynamic.
To wrap useful methods.
To make it reusable without changing a structure.

Lets take it into action.

Initializing

Initialize class by giving data, number of clusters we want, number of iters to loop.
Make attributes of those values.
Take k number of medoids serially for the sake of simplicity.
Prepare random color for each cluster.

class KMedoidsClass:
    def __init__(self,data,k,iters):
        self.data= data
        self.k = k
        self.iters = iters
        self.medoids = np.array([data[i] for i in range(self.k)])
        self.colors = np.array(np.random.randint(0, 255, size =(self.k, 4)))/255
        self.colors[:,3]=1

Distance method

To find distance between data points and medoids.

    def manhattan(self,p1, p2):
        return np.abs((p1[0]-p2[0])) + np.abs((p1[1]-p2[1]))

`get_cost` Method

Just to find the cost minimum cost between the data points and medoids.

    def get_costs(self, medoids):
        tmp_clusters = {i:[] for i in range(len(medoids))}
        cst = 0
        for d in self.data:
            dst = np.array([self.manhattan(d, md) for md in medoids])
            c = dst.argmin()
            tmp_clusters[c].append(d)
            cst+=dst.min()

        tmp_clusters = {k:np.array(v) for k,v in tmp_clusters.items()}
        return tmp_clusters, cst

`fit` Method

This method will implement everything we did in above simple example.

    def fit(self):
        
        samples,_ = self.data.shape

        self.clusters, cost = self.get_costs(data=self.data, medoids=self.medoids)
        count = 0
        

        colors =  np.array(np.random.randint(0, 255, size =(self.k, 4)))/255
        colors[:,3]=1

        plt.title(f"Step : 0")
        [plt.scatter(self.clusters[t][:, 0], self.clusters[t][:, 1], marker="*", s=100,
                                        color = colors[t]) for t in range(self.k)]
        plt.scatter(self.medoids[:, 0], self.medoids[:, 1], s=200, color=colors)
        plt.show()

        while True:
            swap = False
            for i in range(samples):
                if not i in self.medoids:
                    for j in range(self.k):
                        tmp_meds = self.medoids.copy()
                        tmp_meds[j] = i
                        clusters_, cost_ = self.get_costs(data=self.data, medoids=tmp_meds)

                        if cost_<cost:
                            self.medoids = tmp_meds
                            cost = cost_
                            swap = True
                            self.clusters = clusters_
                            print(f"Medoids Changed to: {self.medoids}.")
                            plt.title(f"Step : {count+1}")  
                            [plt.scatter(self.clusters[t][:, 0], self.clusters[t][:, 1], marker="*", s=100,
                                        color = colors[t]) for t in range(self.k)]
                            plt.scatter(self.medoids[:, 0], self.medoids[:, 1], s=200, color=colors)
                            plt.show()
            count+=1

            if count>=self.iters:
                print("End of the iterations.")
                break
            if not swap:
                print("No changes.")
                break

Combine all code

class KMedoidsClass:
    def __init__(self,data,k,iters):
        self.data= data
        self.k = k
        self.iters = iters
        self.medoids = np.array([data[i] for i in range(self.k)])
        self.colors = np.array(np.random.randint(0, 255, size =(self.k, 4)))/255
        self.colors[:,3]=1
    
    def manhattan(self,p1, p2):
        return np.abs((p1[0]-p2[0])) + np.abs((p1[1]-p2[1]))
        
    def get_costs(self, medoids, data):
        tmp_clusters = {i:[] for i in range(len(medoids))}
        cst = 0
        for d in data:
            dst = np.array([self.manhattan(d, md) for md in medoids])
            c = dst.argmin()
            tmp_clusters[c].append(d)
            cst+=dst.min()

        tmp_clusters = {k:np.array(v) for k,v in tmp_clusters.items()}
        return tmp_clusters, cst
    
    def fit(self):
        
        samples,_ = self.data.shape

        self.clusters, cost = self.get_costs(data=self.data, medoids=self.medoids)
        count = 0
        

        colors =  np.array(np.random.randint(0, 255, size =(self.k, 4)))/255
        colors[:,3]=1

        plt.title(f"Step : 0")
        [plt.scatter(self.clusters[t][:, 0], self.clusters[t][:, 1], marker="*", s=100,
                                        color = colors[t]) for t in range(self.k)]
        plt.scatter(self.medoids[:, 0], self.medoids[:, 1], s=200, color=colors)
        plt.show()

        while True:
            swap = False
            for i in range(samples):
                if not i in self.medoids:
                    for j in range(self.k):
                        tmp_meds = self.medoids.copy()
                        tmp_meds[j] = i
                        clusters_, cost_ = self.get_costs(data=self.data, medoids=tmp_meds)

                        if cost_<cost:
                            self.medoids = tmp_meds
                            cost = cost_
                            swap = True
                            self.clusters = clusters_
                            print(f"Medoids Changed to: {self.medoids}.")
                            plt.title(f"Step : {count+1}")  
                            [plt.scatter(self.clusters[t][:, 0], self.clusters[t][:, 1], marker="*", s=100,
                                        color = colors[t]) for t in range(self.k)]
                            plt.scatter(self.medoids[:, 0], self.medoids[:, 1], s=200, color=colors)
                            plt.show()
            count+=1

            if count>=self.iters:
                print("End of the iterations.")
                break
            if not swap:
                print("No changes.")
                break
    

Test it

dt = np.random.randint(0,100, (100,2))
kmedoid = KMedoidsClass(dt,5,5)
kmedoid.fit()

png

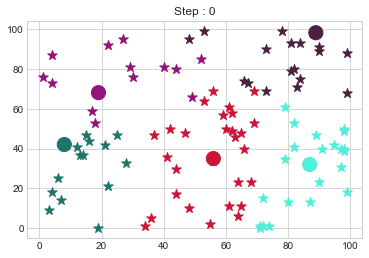
Medoids Changed to: [[10 10]
 [19 68]
 [56 35]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[11 11]
 [19 68]
 [56 35]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[12 12]
 [19 68]
 [56 35]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[13 13]
 [19 68]
 [56 35]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[14 14]
 [19 68]
 [56 35]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [56 35]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [49 49]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [50 50]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [51 51]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [52 52]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [53 53]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [54 54]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [55 55]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [56 56]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [89 98]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [75 75]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [76 76]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [77 77]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [78 78]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [79 79]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [80 80]].

png

Medoids Changed to: [[18 18]
 [19 68]
 [57 57]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[20 20]
 [19 68]
 [57 57]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[21 21]
 [19 68]
 [57 57]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[21 21]
 [19 68]
 [51 51]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[21 21]
 [19 68]
 [52 52]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[21 21]
 [19 68]
 [53 53]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[16 16]
 [19 68]
 [53 53]
 [87 32]
 [81 81]].

png

Medoids Changed to: [[17 17]
 [19 68]
 [53 53]
 [87 32]
 [81 81]].

png

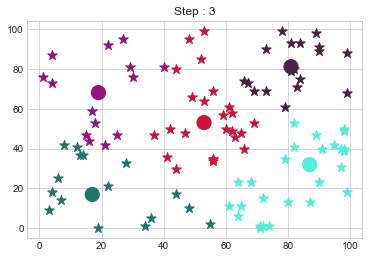
Medoids Changed to: [[18 18]
 [19 68]
 [53 53]
 [87 32]
 [81 81]].

png

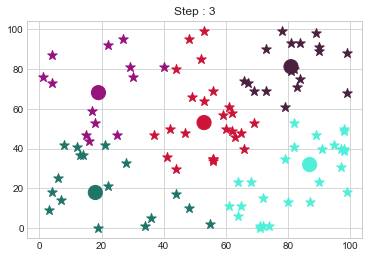
No changes.

Thank you so much for reading this blog. In the next blog, we will do Hierarchical Clustering from Scratch.

Twitter Facebook LinkedIn

K Medoids Clustering in Python from Scratch

Introduction

Durga Pokharel

Introduction

Algorithm

Coding Part

Basic Example

`KMedoids` Class

Initializing

Distance method

`get_cost` Method

`fit` Method

Combine all code

Test it

Comments

You May Also Enjoy

How to do Data Science Project

Mathematics Behind Support Vector Machine

Different method of Outliers Detection

Naive Bayes From Scratch

K Medoids Clustering in Python from Scratch

Introduction

Durga Pokharel

Introduction

Algorithm

Coding Part

Basic Example

KMedoids Class

Initializing

Distance method

get_cost Method

fit Method

Combine all code

Test it

Comments

You May Also Enjoy

How to do Data Science Project

Mathematics Behind Support Vector Machine

Different method of Outliers Detection

Naive Bayes From Scratch

`KMedoids` Class

`get_cost` Method

`fit` Method