DBSCAN Clustering Algorithm

Introduction of Clustering

Clustering is the process of organizing a collection of concrete or abstract things into classes of related objects. A cluster is a group of data objects that are distinct from the objects in other clusters yet comparable to one another within the same cluster. There are various example of clustering algorithm like grouping similar types of document together, clustering can be widely used in outliers detection, where outliers may be more interesting than common cases. The use of outlier detection in electronic commerce and the identification of credit card fraud are two examples of its applications. For instance, unusual credit card transaction scenarios, including particularly expensive and frequent purchases, may be of interest as potential fraud.

How to Check Similarity and Dissimilarity between the data objects.

Distance measurements are employed to determine whether two data objects are similar or dissimilar. The most popular distance measure is Euclidean distance, which is defined as,

\(d(x,y) = \sqrt{(x_2-x_1)^2 + (y_2 - y_1)^2}\) Where x = (x1, y1) and y = (x2, y2).

Another way of calculating distance between objects is Manhattan (or city block) distance is a popular measurement that is defined as

\[d(x,y) = |x_2- x_1| + |y_2 - y_1|\]

A generalization of both Manhattan distance and Euclidean distance is the Minkowski distance. It’s described as

\[d(x,y) = [{(x_2-x_1)^p + (y_2 - y_1)^p}]^\frac{1}{p}\]

Such a distance is also referred to as Lp norm in some literature when p is a positive integer. When p = 1 (i.e., the L1 norm), it represents the Manhattan distance, and when p = 2, the Euclidean distance (i.e., L2 norm).

Categories of Clustering Algorithms

There are numerous clustering algorithms in the literature. The major clustering techniques can generally be divided into the following groups.

Partitioning Methods

A partitioning method creates k partitions of the data from a database containing n objects or data tuples, where each partition represents a cluster and k is less than n. A partitioning method generates an initial partitioning given k, the required number of partitions. After that, an iterative relocation method is used to move items from one group to another in an effort to optimize the partitioning.

Hierarchical Methods

A hierarchical approach divides the provided set of data objects into levels using a hierarchy. There are two types of hierarchical methods: agglomerative and divisive.

The bottom-up strategy is followed by the agglomerative strategy. The first step is for each object to establish a distinct group. It successively merges adjacent objects or groups up until a termination condition is satisfied.

The top-down strategy is followed by the divisive strategy. The entire cluster of things is where it starts. Until a termination condition is met, a cluster is divided into smaller clusters in each subsequent iteration.

Density-based Methods

The majority of object clustering techniques use object distance to group things together. Such algorithms struggle to find clusters of any shape and can only locate spherical-shaped clusters. On the basis of the idea of density, other clustering techniques have been created. They basically want to grow a given cluster as long as the density (number of objects or data points) in the area is above a certain level.

Model-based Methods

Model-based methods posit a model for every cluster and then determine which model best fits the data.

In this blog we are going to discuss briefly about Density Based Clustering Method. OR DBSCAN Clustering Algorithm.

What is DBSCAN Algorithm

DBSCAN is a clustering algorithm based on density. Density based spatial clustering of applications with noise clustering approach is what it stands for. Clusters are dense areas of the data space that are divided by areas of lower density points, according to the DBSCAN algorithm. The fundamental tenet of the DBSCAN algorithm is that each point in a cluster must have at least a certain number of neighbors within a defined radius.

Finding convex or spherical clusters can be done using partitioning techniques and hierarchical clustering. They are only appropriate for clusters that are small and well-distributed. Furthermore, the presence of noise and outliers in the data has a significant impact on them as well. Real-world data, however, could have errors like:

• Clusters can be of arbitrary shape. 
• Data may contain noise. 

The DBSCAN algorithm uses two parameters

• minPTS: The bare minimal quantity of points that must be grouped together—a threshold—for a location to be deemed dense.

• eps: a distance metric that will be used to identify the spots that are close to any given point

In this algorithm we have three types of data Points

• Core Point: If a point has more than MinPts points inside an episodic period, it is a core point.

• Border Point: a point that is close to a core point but has fewer than MinPts inside eps.

• Noise or outlier: A point which is not a core point or border point.

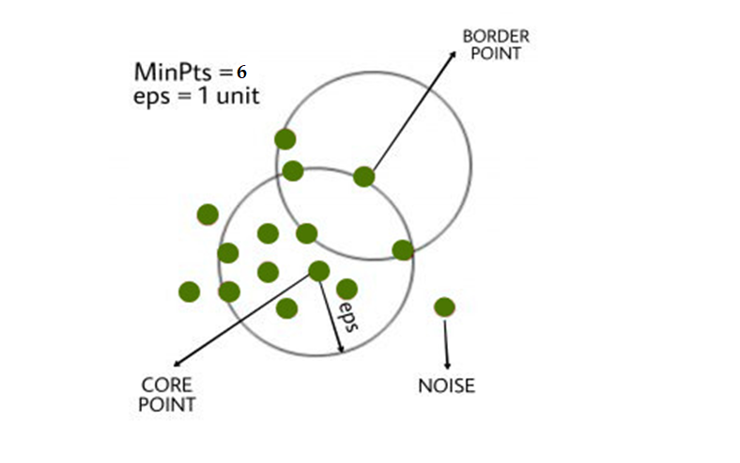
In figure we can see that Core point, Border Point and Noise or outlier. We already discuss idea behind Core point, Border Point and Noise or outlier. We pointed out some points are Core points because they contain the data points equal to or greater number with compared to minPTs values with in given radius. Similarly from definition if there are minimum numbers of points as compared with minPTS threshold with in the given radius then they are pointed as Border point. Points which are neither Core point nor Border Point then they are pointed as noise. Noise are the data points which are different from rest of observations and they diverse fromm the given observations.

Algorithmic Step For DBSCAN Algorithm

• The procedure starts by selecting a point in the dataset at random (until all points have been visited).
• We consider all points to be a part of the same cluster if there are at least minPts points within a radius of to the point.
• The neighborhood calculation is then repeated recursively for each surrounding point to expand the clusters.

How To Apply DBSCAN algorithms into Data Points

Example: Cluster the following data points {(2,10),(2,5),(8,4), (5,8),(7,5),(6,4),(1,2),(4,9)} using DBSCAN algorithm. Assume eps=2 and MinPts=2

Solution:

Let A=(2,10), B=(2,5), C=(8,4), D=(5,8), E=(7,5), F=(6,4), G=(1,2), H=(4,9) First of all we need to findout distance matrix of these data points.

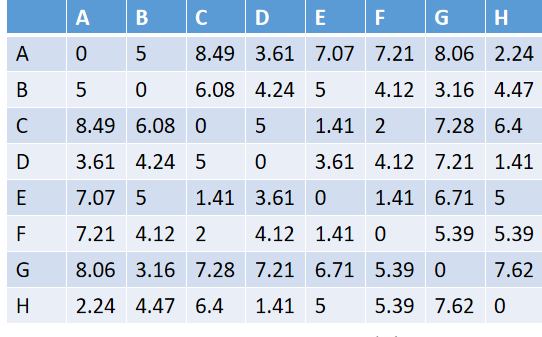
From above distance matrix we can made clusters with the help of given minPTS and eps. So the clusters made are,